Hello, I’m a beginner to registration (1 month experience) and semi-beginner to Python (4 months).
I need to do multiresolution registration in Python with 2D Affine transformation on pairs of 2D fixed and 2D moving images. No images have more than 2 dimensions. I’m currently using SimpleITK 1.2.4 (ITK 4.13), but eventually want to do this in full ITKv4.
The fixed images are binary masks and I wish to transform the moving images to align with these fixed images. The fixed images are generally larger resolution and occupy a larger physical space than the moving images. The moving images can be of any imaging modality, though none are MRI. The moving images have features of varying intensity but are strongly geometrically similar.
All images have different X and Y sizes and could have different X and Y spacing, so each may occupy a different physical 2D space. All images may also have different pixel types.
To set up the code, I’ve largely copied the following sources…
- Chapter 3 Registration of the ITK software guide, although I’m not familiar with C++ so the examples there are hard for me to follow: https://itk.org/ITKSoftwareGuide/html/Book2/ITKSoftwareGuide-Book2ch3.html
- Jupyter Python notebook registration examples 60 to 68: https://github.com/InsightSoftwareConsortium/SimpleITK-Notebooks/tree/master/Python
- Python examples in this beginner Q&A that I found helpful:
https://discourse.itk.org/t/resample-to-same-spacing-and-size-and-align-to-same-origin/1378
… but I’m stuck getting a 2D Affine Transformation to work, partly because the source examples are Euler 3D or some other transformation. Here’s my process and code, which include some questions commented-in:
Dependencies:
import os
import itertools
import SimpleITK as sitk
import matplotlib.pyplot as plt
import numpy as np
import gui
from ipywidgets import interact, fixed
from multiprocessing.pool import ThreadPool
from functools import partial
from IPython.display import display, HTML, clear_output
# Callbacks for plotting registration progress.
import registration_callbacksFirst, I need to define the initial transform and align the centers of the fixed and moving images. For 2D AffineTransform, my understanding is that it requires SetCenter(centerpoint) and not SetOrigin(). I am uncertain where and how to do this for the fixed and moving images simultaneously (if that is required), since they occupy different spaces:
# Make sure to give centerpoint of SetCenter(centerpoint) in world coordinates.
initial_transform = sitk.AffineTransform(sitk.CenteredTransformInitializer(
fixed_image,
moving_image,
sitk.AffineTransform(2), #AffineTransform(2) or AffineTransform()?
sitk.CenteredTransformInitializerFilter.GEOMETRY,
# for centering, something like?:
sitk.SetCenter([fixed_X/2, moving_X/2],[ fixed_Y/2, moving_Y/2]) )) Second, I configure the registration as in the sources above. This code executes without error after defining initial_transform as above, except with the sitk.SetCenter line commented-out:
# This is the registration configuration which we use in all cases. The only parameter that we vary
# is the initial_transform.
def multires_registration(fixed_image, moving_image, initial_transform):
# Registration framework setup.
registration_method = sitk.ImageRegistrationMethod()
# Interpolator (bspline is slowest)
registration_method.SetInterpolator(sitk.sitkLinear)
# Similarity metric settings
registration_method.SetMetricAsMattesMutualInformation(numberOfHistogramBins=50)
registration_method.SetMetricSamplingStrategy(registration_method.RANDOM)
registration_method.SetMetricSamplingPercentage(0.01)
# Optimizer settings
registration_method.SetOptimizerAsGradientDescent(learningRate=1.0, numberOfIterations=100, convergenceMinimumValue=1e-6, convergenceWindowSize=10)
# Scale the step size differently for each parameter
registration_method.SetOptimizerScalesFromPhysicalShift()
# Set the initial moving and optimized transforms in ITKv4.
optimized_transform = sitk.AffineTransform() #AffineTransform(2) dimensions
registration_method.SetMovingInitialTransform(initial_transform)
registration_method.SetInitialTransform(optimized_transform, inPlace=False)
# Setup for the multi-resolution framework.
registration_method.SetShrinkFactorsPerLevel(shrinkFactors = [4,2,1])
registration_method.SetSmoothingSigmasPerLevel(smoothingSigmas = [2,1,0])
registration_method.SmoothingSigmasAreSpecifiedInPhysicalUnitsOn()
# Connect all of the observers so that we can perform plotting during registration.
# NOTE: next 4 lines may have to be moved outside this function definition
registration_method.AddCommand(sitk.sitkStartEvent, registration_callbacks.metric_start_plot)
registration_method.AddCommand(sitk.sitkEndEvent, registration_callbacks.metric_end_plot)
registration_method.AddCommand(sitk.sitkMultiResolutionIterationEvent, registration_callbacks.metric_update_multires_iterations)
registration_method.AddCommand(sitk.sitkIterationEvent, lambda: registration_callbacks.metric_plot_values(registration_method))
# Possibly need to cast fixed and moving images as e.g. sitk.sitkFloat32
final_transform = registration_method.Execute(fixed_image, moving_image)
print('Final metric value: {0}'.format(registration_method.GetMetricValue()))
print('Optimizer\'s stopping condition, {0}'.format(registration_method.GetOptimizerStopConditionDescription()))
print(final_transform)
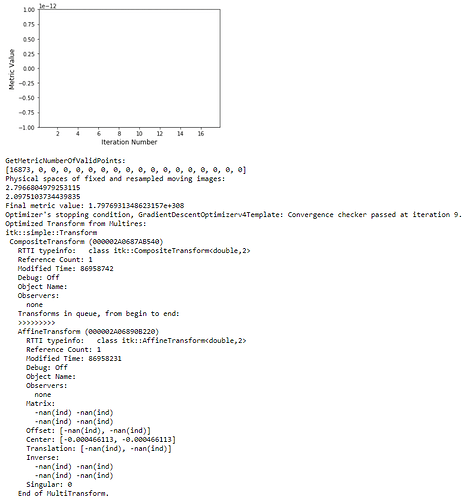
return (final_transform, registration_method.GetMetricValue())Third, I want to find the best initial rotation of the (now centered) moving image from the set of angles: 0, pi/2, pi, 3*pi/2. I don’t expect any moving image to be mirrored, so there’s no need for X- or Y-flipped cases. The code below currently throws the error ‘MattesMutualInformationImageToImageMetricv4(000001DDD7E4F770) Too many samples map outside moving image buffer’. I suspect this is due to the uncentered image pairs that I’m having trouble with, in the First step.
# This function evaluates the metric value in a thread safe manner
def evaluate_metric(current_rotation, tx, f_image, m_image):
print(current_rotation)
registration_method = sitk.ImageRegistrationMethod()
registration_method.SetMetricAsMattesMutualInformation(numberOfHistogramBins=50)
registration_method.SetMetricSamplingStrategy(registration_method.RANDOM)
registration_method.SetMetricSamplingPercentage(0.01)
registration_method.SetInterpolator(sitk.sitkLinear)
current_transform = sitk.AffineTransform(tx)
#from sitk.AffineTransform: Rotate (int axis1, int axis2, double angle, bool pre=false)
current_transform.Rotate(axis1=0, axis2=1, angle=current_rotation)
registration_method.SetInitialTransform(current_transform)
res = registration_method.MetricEvaluate(f_image, m_image)
return res
# 2D orientations
orientations_list = [0,np.pi/2,np.pi, 3*np.pi/2]
p = ThreadPool(len(orientations_list))
all_metric_values = p.map(partial(evaluate_metric,
tx = initial_transform,
f_image = fixed_image,
m_image = moving_image),
orientations_list)
print(all_metric_values)
best_orientation = orientations_list[np.argmin(all_metric_values)]
print('best orientation: {}/'.format(best_orientation))Fourth, I create the reference domain based on the largest possible space in this dataset:
# Create reference domain
dimension=2
# Create the reference image with a zero origin, identity direction cosine matrix and dimension
reference_origin = np.zeros(dimension)
reference_direction = np.identity(dimension).flatten()
reference_size = [512]*dimension # Arbitrary sizes, smallest size that yields desired results.
# Physical image size corresponds to the largest physical size in the training set, or any other arbitrary size, where 'size' = (image_canvas_length-1)*pixel_length in each dimension
#largestphysicalspace(sources) returns [x,y] = [5855.0, 5195.0]
reference_physical_size = largestphysicalspace(sources)
print(reference_physical_size)
reference_spacing = [ phys_sz/(sz-1) for sz,phys_sz in zip(reference_size, reference_physical_size) ]
# Load ith pair of fixed_image and moving_image as target_pair[0] and target_pair[1], and as sitk.sitkFloat32 (pixel type 8)
i = 0
target_pair=loadtargetpair(sources, i, 8)
#Assign the [ith] moving_image [index 1] as the reference_image. [Index 7] contains the pixel type (integer) of the original image:
reference_image = sitk.Image(reference_size, sources[1][i][7])
reference_image.SetOrigin(reference_origin)
reference_image.SetSpacing(reference_spacing)
reference_image.SetDirection(reference_direction)
# Always use the TransformContinuousIndexToPhysicalPoint to compute an indexed point's physical coordinates as
# this takes into account size, spacing and direction cosines. For the vast majority of images the direction
# cosines are the identity matrix, but when this isn't the case simply multiplying the central index by the
# spacing will not yield the correct coordinates resulting in a long debugging session.
reference_center = np.array(reference_image.TransformContinuousIndexToPhysicalPoint(np.array(reference_image.GetSize())/2.0))Fifth, I wish to perform the registration and show the transformed moving_image:
final_transform,_ = multires_registration(fixed_image, moving_image, initial_transform)
#Resample the moving image given the optimized transform, and display
moving_resampled = sitk.Resample(moving_image, fixed_image, final_transform, sitk.sitkLinear, 0.0, moving_image.GetPixelID())
# display_images_with_alpha is as defined in the Utility Functions in the Jupyter notebook 60_Registration_Introduction
interact(display_images_with_alpha, image_z=(0,fixed_image.GetSize()[2] - 1), alpha=(0.0,1.0,0.05), fixed = fixed(fixed_image), moving=fixed(moving_resampled))I know I’m stuck at initializing an Affine 2D transform with centering, and would appreciate suggestions on how to do that. But what else am I missing to get the spine of this registration process working? I realize that my pixel types are a bit mixed up in the code… you can assume all are type sitk.sitkFloat32 for simplicity.
Thank you greatly for your time!
):
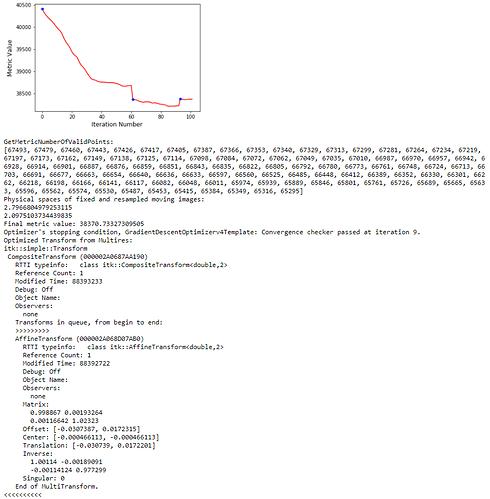
I’ve combined the initial_transform and optimized_transform after registration to get the following 2D Affine registration to work, using your ‘basic’ example and Version 1.1 notebook link:
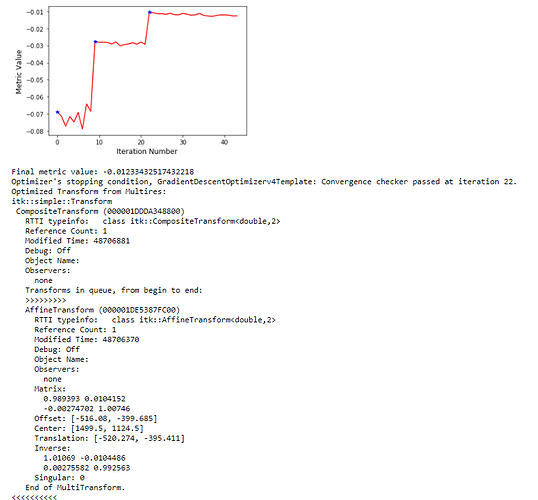
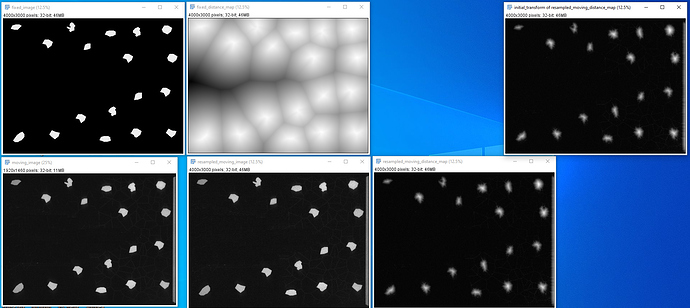
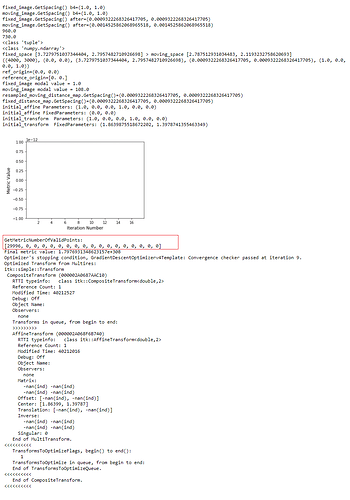
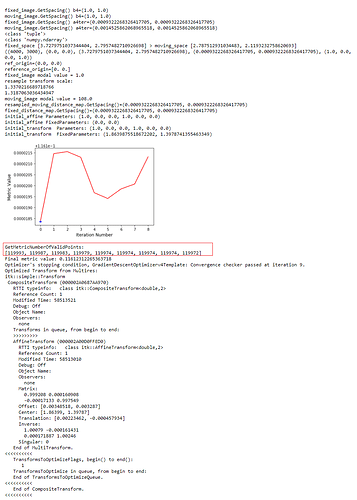
! But multilevel registration still fails due to the same problem in my previous post: no valid points found on the 2nd to Nth iterations.
