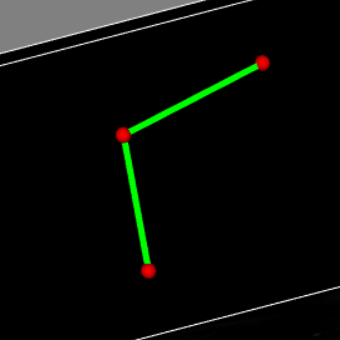
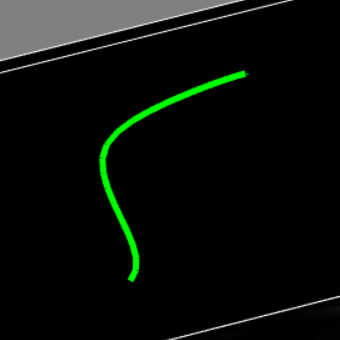
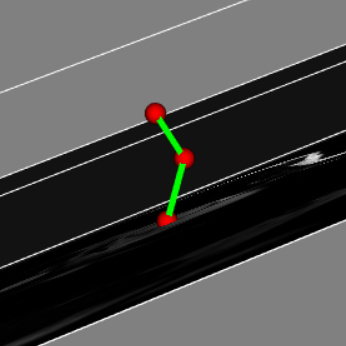
Hello folks,
Once again I need your insight on this matter. I’m trying to fit a closed spline based on user input.
From N user input points describing a contour, I want to sample 30 points on a fitted cubic spline.
Thus the spline order is 3 and the number of control points is 4.
When I use the filter in open dimension mode, just adding the first point also as the last one to mimic a closed curve, everything goes fine, but the quality of fitting around starting point is obviously lower due to the absence of continuity constraint.
My problem is two-fold: when I use the filter with closed dimension, the number of control point need to be at least 7, otherwhile an exception is thrown during update due to this part of code.
// Generate the control point lattice
typename RealImageType::SizeType size;
for( unsigned int i = 0; i < ImageDimension; i++ )
{
if( this->m_CloseDimension[i] )
{
size[i] = this->m_CurrentNumberOfControlPoints[i] - this->m_SplineOrder[i];
}
else
{
size[i] = this->m_CurrentNumberOfControlPoints[i];
}
}
this->m_PhiLattice = PointDataImageType::New(); // <- with closed dimension size is too low with 4 control points
Is that an expected behavior ? From the guide it was not clear, I understood that it was internally a constraint about first and last control points being equals.
Second part of the problem is the result of fitting with closed dimension is really different, visually much more erroneous, and I don’t understand why. Here is the results of the fitting.
a/ open-mode + 4 control points ;
b/ open-mode + 7 CPs (user points located by yellow circles, and result of linear fitting in green) ;
c/ closed-mode + 7 CPs ;
a/
b/
c/
So my question: does a fitting of closed curve requires specific parametrization that I’m obviously missing ?
I’m adding my fitting code below.
N.B. by the way the interface of the filter for just evaluating curve without image doesn’t seem to be possible anymore ? We can deactivate the image generation but Evaluate method is non existant.
std::vector<itk::Vector<double, 2>> InputPoints(UserSelectedPts1.size());//
for (unsigned int i = 0; i < UserSelectedPts1.size(); i++)
{
itk::Vector<double, 2> tmpVect;
tmpVect[0] = UserSelectedPts1[i][0];
tmpVect[1] = UserSelectedPts1[i][1];
InputPoints[i] = tmpVect;
}
// close the contour
{
itk::Vector<double, 2> tmpVect;
tmpVect[0] = UserSelectedPts1[0][0];
tmpVect[1] = UserSelectedPts1[0][1];
InputPoints.push_back(tmpVect);
}
/* itk fitting take the pointset (proto-mesh) structure as input, where the point id serve the parametric dimension whereas the point data is the data dimension
i.e. to fit a line on 2d point, parametric dimension is 1, data dimension is 2
*/
const unsigned int DataDimension = 2, ParametricDimension = 1;
using DataType = itk::Vector<double, DataDimension>;
using ParametricType = itk::Point<float, ParametricDimension>;
using FittingPointSet = itk::PointSet<DataType, ParametricDimension>;
//the bspline filter will output an itk image of ParametricDimension dimension, where pixel are of DataType type
typedef itk::Image<DataType, ParametricDimension> BsplineImageType;
typedef itk::BSplineScatteredDataPointSetToImageFilter<FittingPointSet, BsplineImageType> BSplineFitterType;
//here we define the parametrization of the fitting problem, i.e. the order of points for our line fitting
std::vector<ParametricType> Parametrization(InputPoints.size());
float running_distance = 0;
for (unsigned int i = 0; i < Parametrization.size(); i++)
{
ParametricType pt_p;
if (i!=0)
{
running_distance += sqrt(pow(InputPoints[i][0] - InputPoints[i - 1][0], 2) + pow(InputPoints[i][1] - InputPoints[i - 1][1], 2));
}
pt_p[0] = running_distance;
Parametrization[i] = pt_p;
}
//add the final segment length
//running_distance += sqrt(pow(InputPoints[0][0] - InputPoints[InputPoints.size() - 1][0], 2) + pow(InputPoints[0][1] - InputPoints[InputPoints.size() - 1][1], 2));
/*filling the point set :
we center the points set as the fitting method is sensitive to absolute coordinates
i.e. gives differents results depending on how far from origin (0,0,0) are the parametric points
A better fitting is usually obtained near the origin
*/
FittingPointSet::Pointer PointSet = FittingPointSet::New();
itk::Point<double, 2> Centroid;
Centroid[0] = Centroid[1] = 0;
for (unsigned int i = 0; i < InputPoints.size()-1; i++)
{
Centroid[0] += InputPoints[i][0];
Centroid[1] += InputPoints[i][1];
}
Centroid[0] /= InputPoints.size()-1;
Centroid[1] /= InputPoints.size()-1;
for (unsigned int i = 0; i < InputPoints.size(); i++)
{
PointSet->SetPoint(i, Parametrization[i]);
itk::Vector<double, 2> CenteredPoint;
CenteredPoint[0] = InputPoints[i][0] - Centroid[0];
CenteredPoint[1] = InputPoints[i][1] - Centroid[1];
PointSet->SetPointData(i, CenteredPoint);
}
/* Configuration of the desired spline : use an usual cubic spline (as this minimize the curvature of the fitting)
*/
unsigned int SplineOrder = 3, NbOfLevels = 10;
itk::FixedArray<unsigned int, ParametricDimension> NbControlPoints, ClosedDimension;
NbControlPoints[0] = SplineOrder*2 + 1;
ClosedDimension[0] = 0; //this array is to indicate whether the associated dimension is closed/periodic (1) or not (0)
itk::Size<1> BsplineImageSize;
BsplineImageSize[0] = 31;// 30 points give a out-of-domain exception error -> due to arc length approx by euclidean distance ?
itk::Vector<double, 1> BsplineImageSpacing; //the spacing of output image control in fact the sampling of the continuous spline
BsplineImageSpacing[0] = running_distance/30; //i.e. the arc length needed for regularly spaced 30 points
itk::Point<double, 1> BsplineImageOrigin;
BsplineImageOrigin[0] = 0; //start directly at first input point;
/* Setup and run filter */
BSplineFitterType::Pointer SplineFitter = BSplineFitterType::New();
SplineFitter->SetInput(PointSet);
SplineFitter->SetBSplineEpsilon(1e-3);
SplineFitter->SetSplineOrder(SplineOrder);
SplineFitter->SetNumberOfControlPoints(NbControlPoints);
SplineFitter->SetCloseDimension(ClosedDimension);
SplineFitter->SetNumberOfLevels(NbOfLevels);
SplineFitter->SetOrigin(BsplineImageOrigin);
SplineFitter->SetSpacing(BsplineImageSpacing);
SplineFitter->SetSize(BsplineImageSize);
try
{
SplineFitter->Update();
}
catch (itk::ExceptionObject & err)
{
std::cerr << err;
throw;
}
catch (...)
{
throw Exception("ERROR: Unknown error when trying to run the fitting filter\n");
}
std::vector<itk::ContinuousIndex<double, 2>> ReturnedCI;
itk::ImageRegionConstIterator<BsplineImageType> Parser(SplineFitter->GetOutput(), SplineFitter->GetOutput()->GetLargestPossibleRegion());
while (!Parser.IsAtEnd())
{
itk::Vector<double, 2> CenteredPt = Parser.Get();
itk::ContinuousIndex<double, 2> RetPt;
RetPt[0] = CenteredPt[0] + Centroid[0];
RetPt[1] = CenteredPt[1] + Centroid[1];
ReturnedCI.push_back(RetPt);
++Parser;
}
ReturnedCI.pop_back();


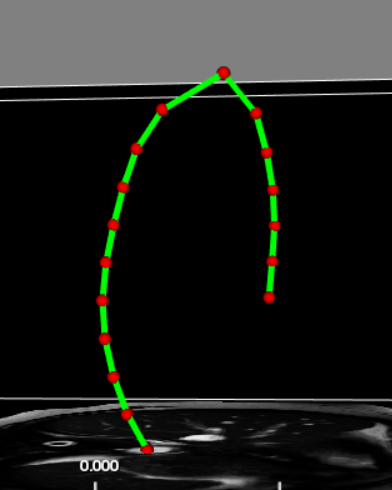

 ) it looks like reducing the spline order may help.
) it looks like reducing the spline order may help.