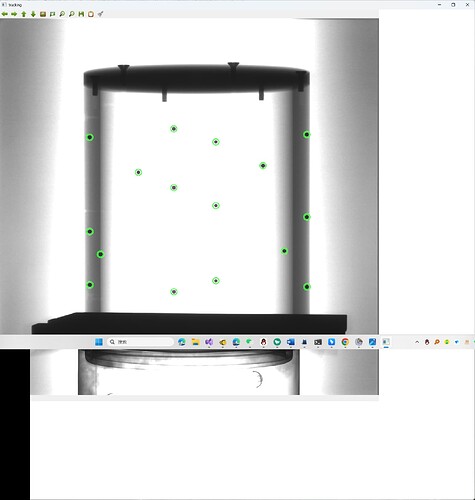
I have a set of images of a phantom with steel balls, and I have extracted the coordinates of the steel balls. In total, there are 845 images, and I have tracked the coordinates of each steel ball. Currently, the known quantities are the coordinates of each steel ball in the 845 images, as well as the three-dimensional coordinates of the steel balls in the phantom. Now, to perform geometric calibration, what should I do? My confusion lies in whether the gantry angle is considered a known quantity or an unknown quantity. I have been unable to obtain results using LM optimization and least squares methods.
> def likelihood(params, A, b):
> inPlaneAngle = params[0]
> outOfPlaneAngle = params[1]
> SourceToDetectorDistance = params[2]
> SourceToIsocenterDistance = params[3]
> sourceOffsetX = params[4]
> sourceOffsetY = params[5]
> projOffsetX = params[6]
> projOffsetY = params[7]
> c = params[8] # 从params中提取c值
> # squared_residuals_sum = 0.0
>
>
>
> # c = c* math.pi / 180.0
> gantryAngle = c # 获取当前点对应的gantryAngle
>
> Rz = np.array([[np.cos(-inPlaneAngle), -np.sin(-inPlaneAngle), 0],
> [np.sin(-inPlaneAngle), np.cos(-inPlaneAngle), 0],
> [0, 0, 1]])
>
> # 绕X轴旋转矩阵
> Rx = np.array([[1, 0, 0],
> [0, np.cos(-outOfPlaneAngle), -np.sin(-outOfPlaneAngle)],
> [0, np.sin(-outOfPlaneAngle), np.cos(-outOfPlaneAngle)]])
>
> # 绕Y轴旋转矩阵
> Ry = np.array([[np.cos(-gantryAngle), 0, np.sin(-gantryAngle)],
> [0, 1, 0],
> [-np.sin(-gantryAngle), 0, np.cos(-gantryAngle)]])
>
> rotation_matrix = np.dot(Rz, np.dot(Rx, Ry))
>
> # 平移向量
> translation_vector = np.zeros((3, 1)) # 这里默认平移向量为 [0, 0, 0]
>
> # 创建齐次矩阵
> homogeneous_matrix = np.eye(4)
> homogeneous_matrix[:3, :3] = rotation_matrix
> homogeneous_matrix[:3, 3] = np.squeeze(translation_vector)
>
> Mp1 = np.array([[1, 0, sourceOffsetX - projOffsetX],
> [0, 1, sourceOffsetY - projOffsetY],
> [0, 0, 1]])
>
> Mp2 = np.array([[-SourceToDetectorDistance, 0, 0, 0],
> [0, -SourceToDetectorDistance, 0, 0],
> [0, 0, 1, -SourceToIsocenterDistance]])
>
> Mp3 = np.array([[1, 0, 0, -sourceOffsetX],
> [0, 1, 0, -sourceOffsetY],
> [0, 0, 1, 0],
> [0, 0, 0, 1]])
>
> Mp = np.dot(Mp1, np.dot(Mp2, np.dot(Mp3, homogeneous_matrix)))
>
>
> projected_points = np.dot(Mp, A.T)
> projected_points /= np.divide(projected_points[2], projected_points[2])
> residuals = projected_points[:2].T - b
> squared_residuals = np.sum(residuals**2)
> # squared_residuals_sum += squared_residuals
> #print(A.shape[0])
> return squared_residuals
This is my modeling of the RTK circular projection geometry, used as an estimation function. However, I have been unable to obtain results using maximum likelihood estimation and least squares methods. I anticipated two outcomes: one is to solve for each parameter, and the other is to obtain a projection matrix corresponding to each angular position. However, I cannot achieve either. Can you help me?
What you might want is OpenCV’s calibrateCamera(), as it provides rotation and translation vectors for each calibration image (tutorial).
thank you very much
However, the modeling approach for the camera is different from the circular geometric modeling approach of RTK. Can these methods be used interchangeably, or do I only need to compute the projection matrix without concerning specific SID and SAD parameters?
Calibrate camera should give your camera positions on a circular path around the phantom. I have not used RTK myself, so I don’t know how to further treat that. Perhaps @simon.rit has some advice?
If you know the position of the source + position and orientation of the detector at each position, you can use AddProjection to create your RTK geometry object.
This won’t work, OpenCV only supports planar calibration
I only know the approximate parameters, so I need to calibrate to determine more accurate results.
I have the same question. In 2d image of ITK, u→,v↓, in a pinhole model and DLT, u→ v↓. But in 3D circular geometry in RTK wiki, RTK: RTK 3D circular projection geometry , u→,v↑ ,the direction of v axis is opposite to 2D image and pinhole model.
I wonder whether I can directly input the projection matrice obtained by DLT and optimization.