3D Affine:Rotate on two different axes one after the other

wic94016 · September 4, 2022, 8:32am

Hey guys,I have a serious question about my python code.
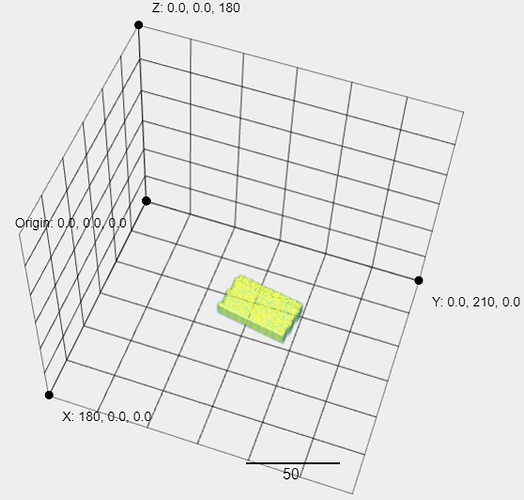
What I want to do is ,if I have a 3D array like this

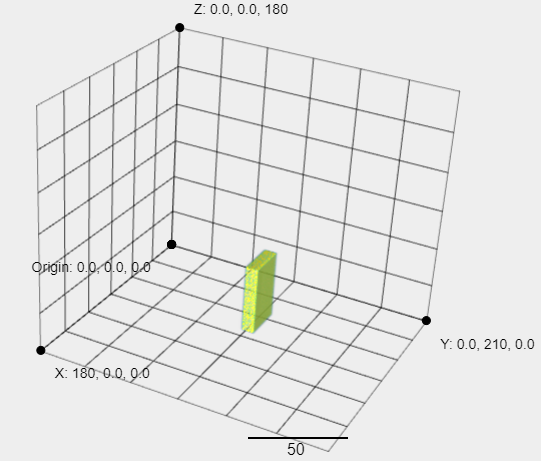
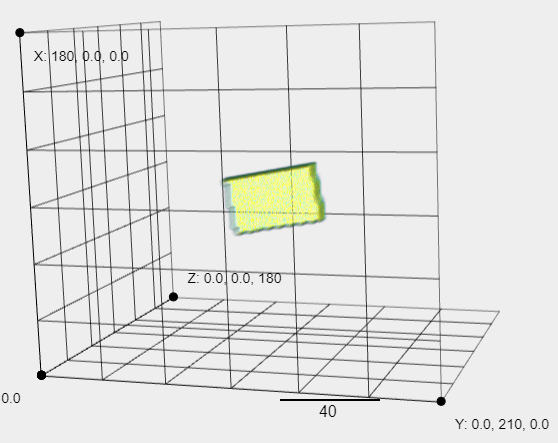
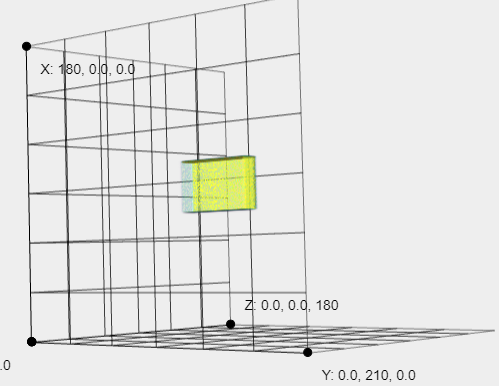
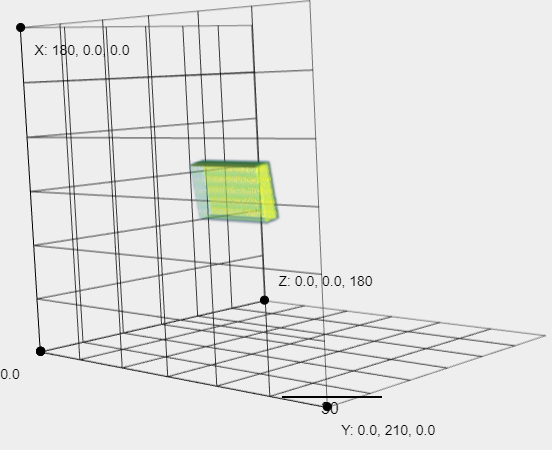
and I want it to be 90 degrees around the -X axis first,then 10 degrees around the y axis.
But it seems to wrap 90 degrees around the -X axis first, then 10 degrees around the z axis.

I don’t know why this is happening, it’s been bothering me for a long time, hope someone can tell me how.

The code below is what I wrote.

degrees1 = 90
rads1 = -(degrees1 )* math.pi / 180
degrees2 = 10
rads2 = -(degrees2 )* math.pi / 180
degrees = 0
rads = degrees * math.pi / 180

u=-1
v=0
w=0
S_mni1=np.array([[u**2+(v**2+w**2)*math.cos(rads1) , u*v*(1-math.cos(rads1))-w*math.sin(rads1) , u*w*(1-math.cos(rads1))+v*math.sin(rads1) , 0],
               [u*v*(1-math.cos(rads1))+w*math.sin(rads1) , v**2+(u**2+w**2)*math.cos(rads1) , v*w*(1-math.cos(rads1))-u*math.sin(rads1) , 0],
               [u*w*(1-math.cos(rads1))-v*math.sin(rads1) , v*w*(1-math.cos(rads1))+u*math.sin(rads1) , w**2+(u**2+v**2)*math.cos(rads1) , 0],
               [0,0,0,1]])

u=0
v=1
w=0
S_mni2=np.array([[u**2+(v**2+w**2)*math.cos(rads2) , u*v*(1-math.cos(rads2))-w*math.sin(rads2) , u*w*(1-math.cos(rads2))+v*math.sin(rads2) , 0],
               [u*v*(1-math.cos(rads2))+w*math.sin(rads2) , v**2+(u**2+w**2)*math.cos(rads2) , v*w*(1-math.cos(rads2))-u*math.sin(rads2) , 0],
               [u*w*(1-math.cos(rads2))-v*math.sin(rads2) , v*w*(1-math.cos(rads2))+u*math.sin(rads2) , w**2+(u**2+v**2)*math.cos(rads2) , 0],
               [0,0,0,1]])

S_mni=S_mni2.dot(S_mni1)

u=S_mni[0][2]
v=S_mni[1][2]
w=S_mni[2][2]
Trot=np.array([[u**2+(v**2+w**2)*math.cos(rads) , u*v*(1-math.cos(rads))-w*math.sin(rads) , u*w*(1-math.cos(rads))+v*math.sin(rads) , 0],
               [u*v*(1-math.cos(rads))+w*math.sin(rads) , v**2+(u**2+w**2)*math.cos(rads) , v*w*(1-math.cos(rads))-u*math.sin(rads) , 0],
               [u*w*(1-math.cos(rads))-v*math.sin(rads) , v*w*(1-math.cos(rads))+u*math.sin(rads) , w**2+(u**2+v**2)*math.cos(rads) , 0],
               [0,0,0,1]])

Msvs=Trot.dot(S_mni)

vx_mni=np.zeros(size_img,dtype=float)
vx_mni[0:50,0:10,0:30]=1 


x=40-1
y=120-1
z=90-1
sz_1=50
sz_2=10
sz_3=30
move=np.array([-math.floor(z-(sz_3/2))-1,-math.floor(y-(sz_2/2))-1,-math.floor(x-(sz_1/2))-1])

img_volume = vx_mni
itk_img_volume = itk.GetImageFromArray(img_volume)
TransformType = itk.AffineTransform[itk.D, 3]
affine_transform = TransformType.New() 
params = itk.OptimizerParameters[itk.D](12)

params[0] = Msvs[0][0].item()
params[1] = Msvs[0][1].item()
params[2] = Msvs[0][2].item()
params[3] = Msvs[1][0].item()
params[4] = Msvs[1][1].item()
params[5] = Msvs[1][2].item()
params[6] = Msvs[2][0].item()
params[7] = Msvs[2][1].item()
params[8] = Msvs[2][2].item()

params[9] = move[0].item()
params[10] = move[1].item()
params[11] = move[2].item()


affine_transform.SetCenter((abs(move[0].item())+(sz_3/2),abs(move[1].item())+(sz_2/2),abs(move[2].item())+(sz_1/2)))
affine_transform.SetParameters(params)
Image3d = type(itk_img_volume)
resamplerType = itk.ResampleImageFilter[Image3d, Image3d]
resampleFilter = resamplerType.New()

interpolatorType = itk.LinearInterpolateImageFunction[Image3d, itk.D]
interpolator = interpolatorType.New()

resampleFilter.SetInput(itk_img_volume)
resampleFilter.SetTransform(affine_transform)
resampleFilter.SetInterpolator(interpolator)
resampleFilter.SetSize(itk_img_volume.GetLargestPossibleRegion().GetSize())
resampleFilter.SetOutputOrigin(itk_img_volume.GetOrigin())
resampleFilter.SetOutputSpacing(itk_img_volume.GetSpacing())

resampleFilter.Update()
movingImage = resampleFilter.GetOutput()

zivy · September 5, 2022, 3:57pm

Hello @wic94016,

Your question is not an ITK/SimpleITK question, it is about specifying rotations using Euler angles.

This can be done using an intrinsic or extrinsic/fixed axis specification which have different effects (what you are experiencing, intrinsic rotation). Please see explanation on wikipedia and possibly this handout which discusses rotation representation in general.

wic94016 · September 6, 2022, 4:44am

hi @zivy
But I have looked up the official documentation of itk AffineTransform,it mentioned “Any two affine transformations may be composed and the result is another affine transformation.”,so I think I can composed a matrix around the X axis and a matrix around the Y axis that is what my code wrote.
Sadly,the result is different,this is bother me…

zivy · September 15, 2022, 2:16pm

Hello @wic94016,

TL;DR
Switch the composition order of your transformations to get what you want.

Long answer:
This has nothing to do with the affine transformation. The documentation is correct, composition of two affine transformations is an affine transformation. This has to do with understanding rotation specification, are you using a fixed extrinsic coordinate system, all transformations are with respect to that coordinate system or an intrinsic one and the transformations are with respect to the object’s coordinate system (which changes after each rotation):

import numpy as np

def R_x(a):
  return np.array([[1, 0 ,0],
                   [0, np.cos(a), -np.sin(a)],
                   [0, np.sin(a), np.cos(a)]])
def R_y(a):
  return np.array([[np.cos(a), 0, np.sin(a)],
                   [0, 1, 0],
                   [-np.sin(a), 0, np.cos(a)]])

x_angle = np.radians(-90) # equivalent to 90 degree rotation around -x
y_angle = np.radians(90)

print("intrinsic:")
print(np.dot(R_x(x_angle), R_y(y_angle)))

print("extrinsic/fixed:")
print(np.dot(R_y(y_angle), R_x(x_angle)))

wic94016 · September 18, 2022, 7:09am

@zivy
I’m sure the composition order of transformations,like below

# This is a matrix of rotation around -x
u=-1
v=0
w=0
R_x=np.array([[u**2+(v**2+w**2)*math.cos(rads1) , u*v*(1-math.cos(rads1))-w*math.sin(rads1) , u*w*(1-math.cos(rads1))+v*math.sin(rads1) , 0],
               [u*v*(1-math.cos(rads1))+w*math.sin(rads1) , v**2+(u**2+w**2)*math.cos(rads1) , v*w*(1-math.cos(rads1))-u*math.sin(rads1) , 0],
               [u*w*(1-math.cos(rads1))-v*math.sin(rads1) , v*w*(1-math.cos(rads1))+u*math.sin(rads1) , w**2+(u**2+v**2)*math.cos(rads1) , 0],
               [0,0,0,1]])

# This is a matrix of rotation around y
u=0
v=1
w=0
R_y=np.array([[u**2+(v**2+w**2)*math.cos(rads2) , u*v*(1-math.cos(rads2))-w*math.sin(rads2) , u*w*(1-math.cos(rads2))+v*math.sin(rads2) , 0],
               [u*v*(1-math.cos(rads2))+w*math.sin(rads2) , v**2+(u**2+w**2)*math.cos(rads2) , v*w*(1-math.cos(rads2))-u*math.sin(rads2) , 0],
               [u*w*(1-math.cos(rads2))-v*math.sin(rads2) , v*w*(1-math.cos(rads2))+u*math.sin(rads2) , w**2+(u**2+v**2)*math.cos(rads2) , 0],
               [0,0,0,1]])

final_m=R_y.dot(R_x)

Then I used the “final_m” matrix as my rotation matrix.
And if degree is

degrees1 = 90
rads1 = -(degrees1 )* math.pi / 180

degrees2 = 10
rads2 = -(degrees2 )* math.pi / 180

The result wiil be below(Let’s call it “result_XY”)

But if I first use the matrix of rotation around -x as my rotation matrix,
the result like below(Let’s call it “result_x”)

Then I use the matrix of rotation around y as my rotation matrix,
to rotation “result_x”,the result like blow(Let’s call it “result_x_y”)

Why the result_x_y and the result_XY are different?

dzenanz · September 19, 2022, 8:01pm

The resulting compound rotation depends on the order of single axis rotations.

wic94016 · September 21, 2022, 8:43am

Hi @dzenanz
May I ask how can I do external rotation in python with itk?

dzenanz · September 21, 2022, 12:11pm

There are many transform types in ITK. Find the simplest one which can do what you want, and use that.

You did not really explain what you want to accomplish. With rotations, it is usually easiest to compose transforms. Translate so the object is at the coordinate origin, rotate, then translate back. Otherwise the results are usually unintuitive.