SimpleITK: Registration working but applying the transform to a single point does not

[Bouthros]

Hi!

I hope I am putting this question in the proper category.

I followed the Jupyter notebook concerning the 3D registration and I tried to apply it to my problem.

Here is my problem: I have 2 axial series, 1 fixed and 1 moving. The idea is to click on a voxel of the moving series and to display the equivalent position in the fixed series.
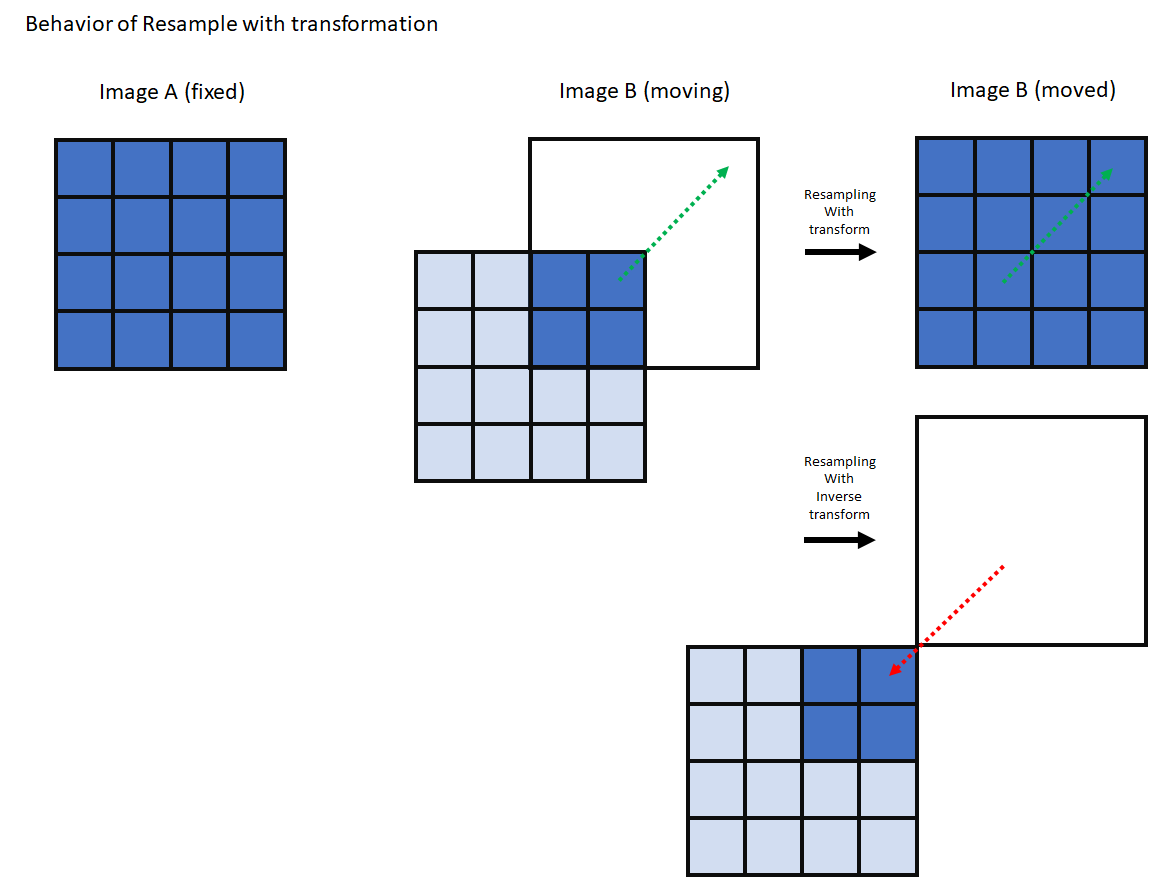
To do so, I decided to take the moving series and register it onto the fixed series. That way I obtain a transformation that is able to compute the voxel position of the moving series to the fixed series.

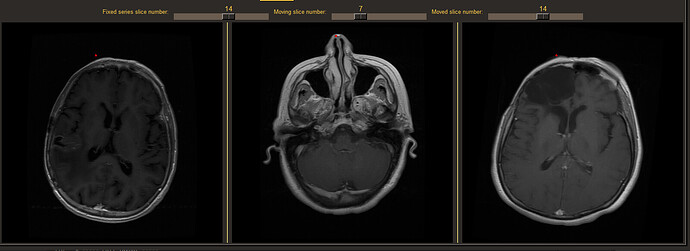
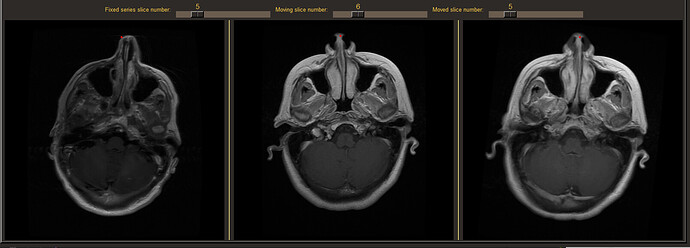
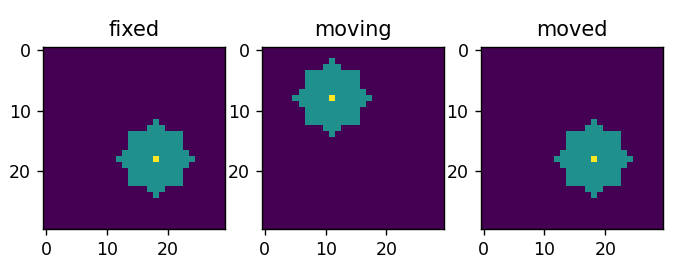
Here is an example:

From left to right, you can see, the fixed series (left), the moving series (middle) and the moved series (right).
The problem I have is when i click on the nose of the moving series (middle), the computation of the location of the pixel on the fixed series is erroneous.

• Moving point [241, 31, 6]
• Moved point [211, 73, 13]

I would have expected the moved point to be [280, 60, 4]
I suppose I made a mistake but I cannot see it. Therefore, I need you help determining how I could fix it.

Here is the full code:

import SimpleITK as sitk

def registration_3d(fixed_image, moving_image):
    
    # Initial Alignment
    # Use the CenteredTransformInitializer to align the centers of the two volumes and set the center of rotation to the center of the fixed image
    initial_transform = sitk.CenteredTransformInitializer(
        fixed_image,
        moving_image,
        sitk.Euler3DTransform(),
        sitk.CenteredTransformInitializerFilter.GEOMETRY,
        )

    # Registration
    registration_method = sitk.ImageRegistrationMethod()

    # Similarity metric settings.
    registration_method.SetMetricAsMattesMutualInformation(numberOfHistogramBins=50)
    registration_method.SetMetricSamplingStrategy(registration_method.RANDOM)
    registration_method.SetMetricSamplingPercentage(0.01)

    registration_method.SetInterpolator(sitk.sitkLinear)

    # Optimizer settings.
    registration_method.SetOptimizerAsGradientDescent(
        learningRate=0.5,
        numberOfIterations=100,
        convergenceMinimumValue=1e-10,
        convergenceWindowSize=10,
    )
    registration_method.SetOptimizerScalesFromPhysicalShift()

    # Setup for the multi-resolution framework.
    registration_method.SetShrinkFactorsPerLevel(shrinkFactors=[4, 2, 1])
    registration_method.SetSmoothingSigmasPerLevel(smoothingSigmas=[2, 1, 0])
    registration_method.SmoothingSigmasAreSpecifiedInPhysicalUnitsOn()

    # Don't optimize in-place, we would possibly like to run this cell multiple times.
    # registration_method.SetInitialTransform(initial_transform, inPlace=False)
    registration_method.SetInitialTransform(initial_transform, inPlace=False)

    final_transform = registration_method.Execute(
        sitk.Cast(fixed_image, sitk.sitkFloat32), sitk.Cast(moving_image, sitk.sitkFloat32)
    )

    # Post registration analysis
    print(f"Final metric value: {registration_method.GetMetricValue()}")
    print(
        f"Optimizer's stopping condition, {registration_method.GetOptimizerStopConditionDescription()}"
    )
    
    moving_resampled = sitk.Resample(
        moving_image,
        fixed_image,
        final_transform,
        sitk.sitkLinear,
        0.0,
        moving_image.GetPixelID(),
    )
    
    return moving_resampled, [initial_transform, final_transform]

reader = sitk.ImageSeriesReader()
dicom_files = reader.GetGDCMSeriesFileNames("C:/test_dirs/DCM/ACQ1_24img")
reader.SetFileNames(dicom_files)
fixed_image = reader.Execute()
fixed_image = sitk.Cast(fixed_image, sitk.sitkFloat32)

reader = sitk.ImageSeriesReader()
dicom_files = reader.GetGDCMSeriesFileNames("C:/test_dirs/DCM/ACQ1_24img_2")
reader.SetFileNames(dicom_files)
moving_image = reader.Execute()
moving_image = sitk.Cast(moving_image, sitk.sitkFloat32)

moved, [init_transform, final_transform] = registration_3d(fixed_image, moving_image)

sitk.Show(fixed_image, "Fixed")
sitk.Show(moving_image, "Moving")
sitk.Show(moved, "Moved")

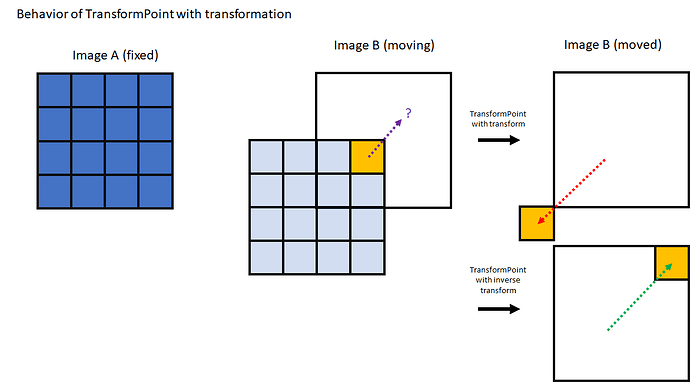
point_init_index = [241, 31, 6]
p_init = moving_image.TransformContinuousIndexToPhysicalPoint([point_init_index[0], point_init_index[1], point_init_index[2]])
p_final = final_transform.TransformPoint(p_init)
p_final_index = moved.TransformPhysicalPointToIndex(p_final)

print(f'Moving point {point_init_index}')
print(f'Moved point {p_final_index}')

Thanks in advance!

PS: I do not know how to upload series if you needed to test with my data. Do not hesitate to tell me how to do it if needed.

[Bouthros]

I guess I got karma’d.
Right after posting it, I found the solution…

I rewatch one of the tutorials : 21_Transforms_and_Resampling
Here is a quote: It important to keep in mind that a transform in a resampling operation defines the transform from the output space to the input space.

The solution was to apply the inverse of the transform:

point_init_index = [241, 31, 6]

final_transform = final_transform.GetInverse()

p_init = moving_image.TransformContinuousIndexToPhysicalPoint([point_init_index[0], point_init_index[1], point_init_index[2]])
p_final = final_transform.TransformPoint(p_init)
p_final_index = moved.TransformPhysicalPointToIndex(p_final)

The results are clearly better:

Sorry for the inconvenience. Maybe it will help a poor soul like me

[dsitk]

@Bouthros

It important to keep in mind that a transform in a resampling operation defines the transform from the output space to the input space.

I don’t correctly understand what the above statement means. If we have a 4x4 transformation matrix, do we need to get its inverse and give that inverted-matrix as the transform matrix to SimpleITK?
Or, does the rotation matrix remain same, and do we need to invert the translation part of the transform?

Even in the 21_Transforms_and_Resampling, why did that grid move towards bottom/left instead of top/right? For a positive translation in LPS coordinates with origin at the bottom-left, shouldn’t that grid move in the opposite direction?

[Bouthros]

My understanding is totally empirical so I will try to answer you but do not hesitate to correct me if I’m wrong.

If you have an image B (moving) that you want to register onto an image A (fixed), the registration method will give you a transformation as output. This transformation corresponds to the movement from physical space A towards physical space B.

If you do a resampling using this transform, the function Resample will do its own magic and will move the Image B in the same physical space than the Image A.

However, if you use the function transform.TransformPoint(point_in_imageB), it will apply the transformation as is. If you want to have the same behavior than the resample, you need to use inverseTransform.TransformPoint(point_in_imageB) with inverseTransform = transform.GetInverse()

In the case of the tutorial, you want to do a translation in a given direction so you need to take the inverse translation and do a TransformPoint with it to go towards the good direction.

I tried to be as clear as possible in my explaination. Tell me if I could answer your questions.

[dsitk]

@Bouthros Thank you for the detailed answer.

The sign-change of translation is just confusing. Here is an example where we want to move this star shape centered at [8, 11] to a new center at [18, 18]. Everything is in world coordinates and not pixel space.

• Fixed Star is centered at [18, 18].
• Moving Star is centered at [8, 11].
• I’d expected Translation component to be [Fixed_Center - Moving_Center].
  T = FC - MC = [18, 18] - [11, 11] = [10, 7]

When we use resample function though, the image just moves in the opposite direction.

import numpy as np
import SimpleITK as sitk
from skimage.morphology import star


def generate_transformation_matrix(angle_degrees, translation=[0, 0]):
    radians = angle_degrees * np.pi / 180.

    cos_theta = np.cos(radians)
    sin_theta = np.sin(radians)
    T = translation

    matrix = np.array([[cos_theta, -sin_theta, T[0]],
                       [sin_theta,  cos_theta, T[1]],
                       [0,          0,         1]])

    return matrix

def sitk_tform_resample(sitk_im, transform, background=0.0):
    im_dim = sitk_im.GetDimension()

    sitk_transform = sitk.Euler2DTransform()
    sitk_transform.SetCenter(sitk_im.GetOrigin())
    sitk_transform.SetMatrix(transform[0:im_dim,0:im_dim].flatten().tolist())
    sitk_transform.SetTranslation(transform[0:im_dim, im_dim])
    print("\nsitk_transform\n", sitk_transform)

    ref_img = sitk_im

    resampled_im = sitk.Resample(sitk_im,
                                 ref_img,
                                 sitk_transform,
                                 sitk.sitkNearestNeighbor, # ~ sitk.sitkLinear,
                                 background)


    return resampled_im

if __name__=='__main__':
    # moving
    mov_im = np.zeros((30, 30))
    mov_im[2:15, 5:18] = star(4)

    mov_im_obj_idx = np.array(np.where(mov_im)).T
    mov_im_obj_center = np.mean(mov_im_obj_idx, axis=0).astype(np.uint8)
    mov_im[tuple(mov_im_obj_center)] = 2

    # fixed
    fix_im = np.zeros((30, 30))
    fix_im[12:25, 12:25] = star(4)

    fix_im_obj_idx = np.array(np.where(fix_im)).T
    fix_im_obj_center = np.mean(fix_im_obj_idx, axis=0).astype(np.int64).tolist()
    fix_im[tuple(fix_im_obj_center)] = 2

    # translation transform
    translation = fix_im_obj_center - mov_im_obj_center
    transform = generate_transformation_matrix(0, translation)

    # simple itk image
    sitk_im = sitk.GetImageFromArray(mov_im)
    sitk_im.SetOrigin([0., 0.])
    sitk_im.SetSpacing([1., 1.])
    sitk_im.SetDirection([1, 0, 0, 1])

    # resample
    translated_im = sitk_tform_resample(sitk_im, transform)

    translated_arr = sitk.GetArrayFromImage(translated_im)
    translated_im_obj_idx = np.array(np.where(translated_arr)).T
    translated_im_obj_center = np.mean(translated_im_obj_idx, axis=0).astype(np.int64)

    print("Fixed Center", fix_im_obj_center, sitk_im.TransformIndexToPhysicalPoint([fix_im_obj_center[0], fix_im_obj_center[1]]))
    print("Initial Moving Center", mov_im_obj_center)
    print("New Moving Center", translated_im_obj_center)

I’m missing something with coordinate systems. If sitk_im has been created correctly above, would you expect the above translation to be accurate in world coordinates?

[Bouthros]

OK, so I took your code and I found what was missing.

1. First one was here:

@dsitk

matrix = np.array([[cos_theta, -sin_theta, T[0]],
                   [sin_theta,  cos_theta, T[1]],
                   [0,          0,         1]])

You forgot that you determine the translation using numpy coordinates (Y,X). So i swapped T[0] and T[1] to have a (X,Y) array and to use this matrix instead:

@Bouthros

matrix = np.array([[cos_theta, -sin_theta, T[1]],
                   [sin_theta,  cos_theta, T[0]],
                   [0,          0,         1]])

2. Here is the second mistake

@dsitk

translation = fix_im_obj_center - mov_im_obj_center

As explained in ITK registration description:

The transform component T (X) represents the spatial mapping of points from the fixed image space to points in the moving image space.

We want the translation from the fixed image towards the moving image as input for the Resample function.

@Bouthros

translation = mov_im_obj_center - fix_im_obj_center

For exemple, this could be the result of an automatic registration such as my initial problem and that is what I tried to explain with this phrase:

@Bouthros

If you have an image B (moving) that you want to register onto an image A (fixed), the registration method will give you a transformation as output. This transformation corresponds to the movement from physical space A towards physical space B.

3. With these two corrections, boom, you get what you want:
   
   

Translation: [-10, -7]

Fixed Center [18, 18] (18.0, 18.0)
Initial Moving Center [ 8 11]
New Moving Center [18 18]

By extension, if you even wanted to use the TransformPoint to determine a point from moving to fixed, you would need to do as such:

@Bouthros

point_in_fixed = sitk_transform.GetInverse().TransformPoint(point_in_moving)

EDIT: I corrected my version of the translation, i copied and pasted your code instead of mine, sorry
EDIT2: added more info
EDIT3: last edit for the night , added link to ITK documentation

[dsitk]

Thanks so much @Bouthros, you’re a life saver!
We basically want the transform going from Fixed image to Moving image, and we need to give this transform as input to ‘Resample’ API.