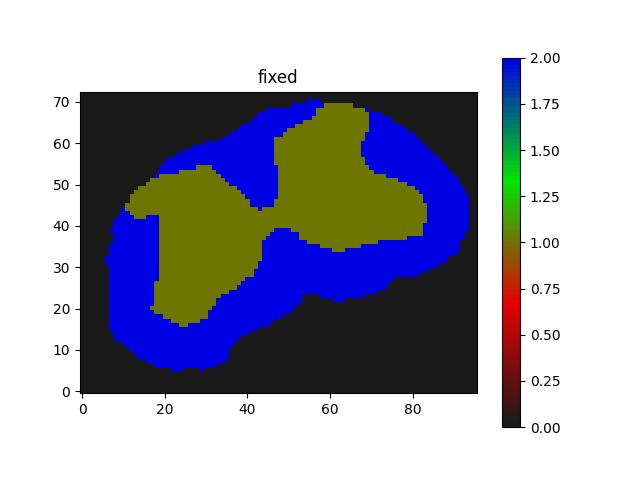
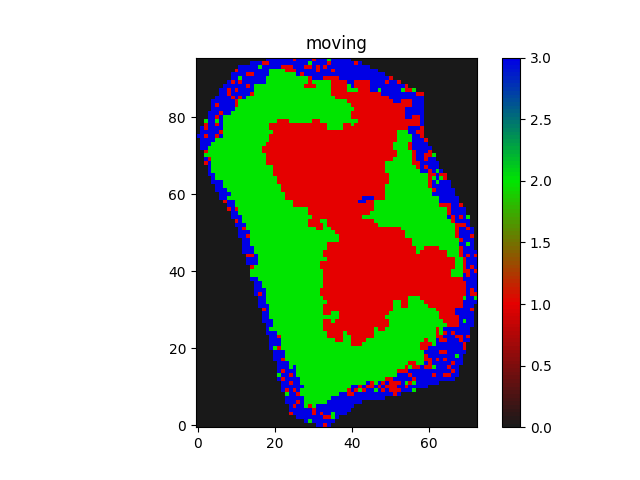
I am trying to apply Euler2D rotation with Affine registration in an iterative manner.
Something done here https://itk.org/ITKSoftwareGuide/html/Book2/ITKSoftwareGuide-Book2ch3.html#x26-110175r30 at section 3.6.5.
Now I couldn’t find a python version of the example there.
This is the first Euler method:
all_orientations = np.linspace(-2*np.pi, 2*np.pi, 100)
# print(all_orientations)
# Evaluate the similarity metric using the rotation parameter space sampling, translation remains the same for all.
initial_transform = sitk.Euler2DTransform(sitk.CenteredTransformInitializer(fixed_image,
moving_image,
sitk.Euler2DTransform(),
sitk.CenteredTransformInitializerFilter.GEOMETRY))
# Registration framework setup.
registration_method = sitk.ImageRegistrationMethod()
registration_method.SetMetricAsMattesMutualInformation(numberOfHistogramBins=500)
registration_method.SetMetricSamplingStrategy(registration_method.RANDOM)
registration_method.SetMetricSamplingPercentage(0.001)
registration_method.SetInitialTransform(initial_transform, inPlace=False)
registration_method.SetOptimizerAsRegularStepGradientDescent(learningRate=2.0,
minStep=1e-4,
numberOfIterations=500,
gradientMagnitudeTolerance=1e-8)
registration_method.SetInterpolator(sitk.sitkNearestNeighbor)
registration_method.SetOptimizerScalesFromIndexShift()
# best_orientation = (0.0, 0.0)
best_similarity_value = registration_method.MetricEvaluate(fixed_image, moving_image)
similarity_value = []
# Iterate over all other rotation parameter settings.
for key, orientation in enumerate(all_orientations): # .items():
initial_transform.SetAngle(orientation)
registration_method.SetInitialTransform(initial_transform)
current_similarity_value = registration_method.MetricEvaluate(fixed_image, moving_image)
similarity_value.append(current_similarity_value)
# print("current similarity value: ", current_similarity_value)
if current_similarity_value <= best_similarity_value:
best_similarity_value = current_similarity_value
best_orientation = orientation
# else:
# best_orientation = orientation
print('best orientation is: ' + str(best_orientation))
print(current_similarity_value)
plt.plot(all_orientations, similarity_value, 'b')
plt.plot(best_orientation, best_similarity_value, 'rv')
plt.show()
initial_transform.SetAngle(best_orientation)
registration_method.SetInitialTransform(initial_transform, inPlace=False)
eulerTx = registration_method.Execute(fixed_image, moving_image)
resampler = sitk.ResampleImageFilter()
resampler.SetReferenceImage(fixed_image)
resampler.SetInterpolator(sitk.sitkNearestNeighbor)
resampler.SetDefaultPixelValue(0)
resampler.SetTransform(eulerTx)
out = resampler.Execute(moving_image)
del registration_method, initial_transform, eulerTx
moving_image = sitk.Cast(out, sitk.sitkFloat32)
The Euler2D orientation works.
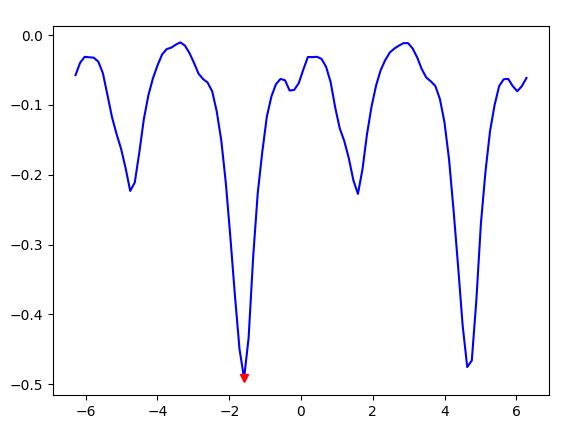
As the best orientation converges at lowest metric with satisfactory visual checkerboard result.
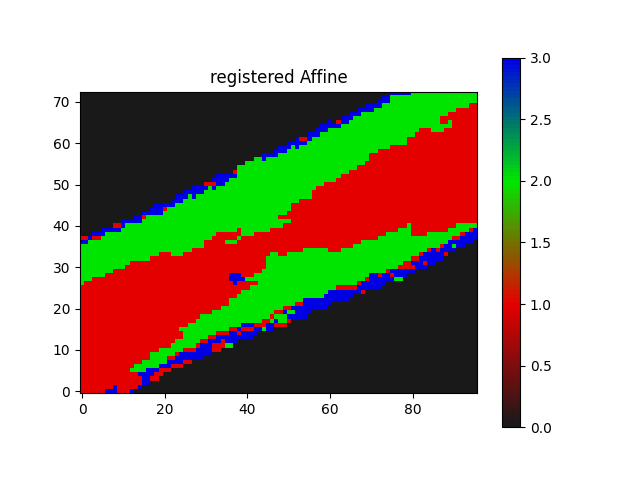
Now how do I run the Affine transformation from here?
I tried the following:
def command_iteration2(method):
global metric_values
print("metric value: {}".format(method.GetMetricValue()))
metric_values.append(method.GetMetricValue())
metric_values = []
initial_transform = sitk.CenteredTransformInitializer(fixed_image,
moving_image,
sitk.AffineTransform(2),
sitk.CenteredTransformInitializerFilter.GEOMETRY)
registration_method = sitk.ImageRegistrationMethod()
registration_method.SetInterpolator(sitk.sitkNearestNeighbor)
registration_method.SetInitialTransform(initial_transform, inPlace=True)
registration_method.SetMetricSamplingStrategy(registration_method.NONE)
# registration_method.SetOptimizerAsGradientDescent(lear)
translationScale = 1.0 / 100.0
registration_method.SetOptimizerAsRegularStepGradientDescent(learningRate=1.0, minStep=1e-4,
numberOfIterations=100)
registration_method.SetOptimizerScales(scales=[1.0, 1.0, 1.0, 1.0, translationScale, translationScale])
registration_method.AddCommand(sitk.sitkIterationEvent, lambda: command_iteration2(registration_method))
final_transform = registration_method.Execute(fixed_image, moving_image)
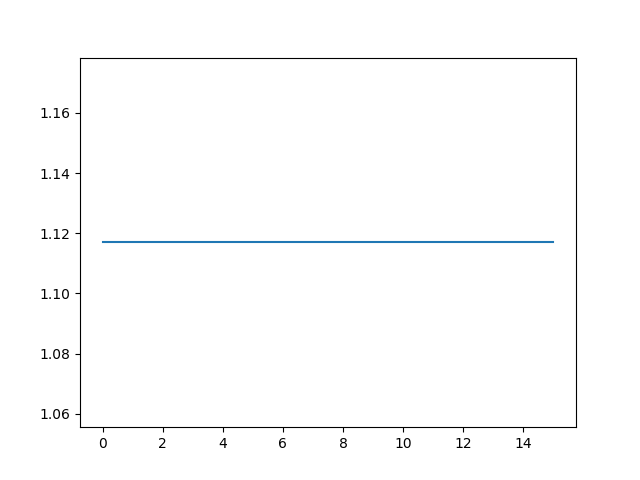
plt.plot(metric_values)
plt.show()
print('Optimizer\'s stopping condition, {0}'.format(registration_method.GetOptimizerStopConditionDescription()))
It gives me the following without any metric plot,
Optimizer's stopping condition, RegularStepGradientDescentOptimizerv4: Gradient magnitude tolerance met after 0 iterations. Gradient magnitude (2.39075e-14) is less than gradient magnitude tolerance (0.0001).
I am a new ITK user so knowing where I am going wrong would be helpful.